Преобразование графиков. Преобразования графиков Преобразование графиков

Основные элементарные функции в чистом виде без преобразования встречаются редко, поэтому чаще всего приходится работать с элементарными функциями, которые получили из основных с помощью добавления констант и коэффициентов. Такие графики строятся при помощи геометрических преобразований заданных элементарных функций.

Рассмотрим на примере квадратичной функции вида y = - 1 3 x + 2 3 2 + 2 , графиком которой является парабола y = x 2 , которая сжата втрое относительно О у и симметрична относительно О х, причем сдвинутую на 2 3 по О х вправо, на 2 единицы по О у вверх. На координатной прямой это выглядит так:

Yandex.RTB R-A-339285-1

Геометрические преобразования графика функции

Применяя геометрические преобразования заданного графика получаем, что график изображается функцией вида ± k 1 · f (± k 2 · (x + a)) + b , когда k 1 > 0 , k 2 > 0 являются коэффициентами сжатия при 0 < k 1 < 1 , 0 < k 2 < 1 или растяжения при k 1 > 1 , k 2 > 1 вдоль О у и О х. Знак перед коэффициентами k 1 и k 2 говорит о симметричном отображении графика относительно осей, a и b сдвигают ее по О х и по О у.

Определение 1

Существует 3 вида геометрических преобразований графика :

• Масштабирование вдоль О х и О у. На это влияют коэффициенты k 1 и k 2 при условии не равности 1 , когда 0 < k 1 < 1 , 0 < k 2 < 1 , то график сжимается по О у, а растягивается по О х, когда k 1 > 1 , k 2 > 1 , то график растягивается по О у и сжимается по О х.
• Симметричное отображение относительно координатных осей. При наличии знака « - » перед k 1 симметрия идет относительно О х, перед k 2 идет относительно О у. Если « - » отсутствует, тогда пункт при решении пропускается;
• Параллельный перенос (сдвиг) вдоль О х и О у. Преобразование производится при наличии коэффициентов a и b неравных 0 . Если значение a положительное, до график сдвигается влево на | а | единиц, если отрицательное a , тогда в право на такое же расстояние. Значение b определяет движение по оси О у, что значит при положительном b функция движется вверх, при отрицательном – вниз.

Рассмотрим решения на примерах, начиная со степенной функции.

Пример 1

Преобразовать y = x 2 3 и построить график функции y = - 1 2 · 8 x - 4 2 3 + 3 .

Решение

Представим функции таким образом:

y = - 1 2 · 8 x - 4 2 3 + 3 = - 1 2 · 8 x - 1 2 2 3 + 3 = - 2 x - 1 2 2 3 + 3

Где k 1 = 2 , стоит обратить внимание на наличие « - » , а = - 1 2 , b = 3 . Отсюда получаем, что геометрические преобразования производятся с растяжения вдоль О у вдвое, отображается симметрично относительно О х, сдвигается вправо на 1 2 и вверх на 3 единицы.

Если изобразить исходную степенную функцию, получим, что

при растягивании вдвое вдоль О у имеем, что

Отображение, симметричное относительно О х, имеет вид

а движение вправо на 1 2

движение на 3 единицы вверх имеет вид

Преобразования показательной функции рассмотрим на примерах.

Пример 2

Произвести построение графика показательной функции y = - 1 2 1 2 (2 - x) + 8 .

Решение.

Преобразуем функцию, исходя из свойств степенной функции. Тогда получим, что

y = - 1 2 1 2 (2 - x) + 8 = - 1 2 - 1 2 x + 1 + 8 = - 1 2 · 1 2 - 1 2 x + 8

Отсюда видно, что получим цепочку преобразований y = 1 2 x:

y = 1 2 x → y = 1 2 · 1 2 x → y = 1 2 · 1 2 1 2 x → → y = - 1 2 · 1 2 1 2 x → y = - 1 2 · 1 2 - 1 2 x → → y = - 1 2 · 1 2 - 1 2 x + 8

Получаем, что исходная показательная функция имеет вид

Сжимание вдвое вдоль О у дает

Растягивание вдоль О х

Симметричное отображение относительно О х

Отображение симметрично относительно О у

Сдвигание на 8 единиц вверх

Рассмотрим решение на примере логарифмической функции y = ln (x) .

Пример 3

Построить функцию y = ln e 2 · - 1 2 x 3 при помощи преобразования y = ln (x) .

Решение

Для решения необходимо использовать свойства логарифма, тогда получаем:

y = ln e 2 · - 1 2 x 3 = ln (e 2) + ln - 1 2 x 1 3 = 1 3 ln - 1 2 x + 2

Преобразования логарифмической функции выглядят так:

y = ln (x) → y = 1 3 ln (x) → y = 1 3 ln 1 2 x → → y = 1 3 ln - 1 2 x → y = 1 3 ln - 1 2 x + 2

Изобразим график исходной логарифмической функции

Производим сжимание строе по О у

Производим растягивание вдоль О х

Производим отображение относительно О у

Производим сдвигание вверх на 2 единицы, получаем

Для преобразования графиков тригонометрической функциинеобходимо подгонять под схему решения вида ± k 1 · f (± k 2 · (x + a)) + b . Необходимо, чтобы k 2 приравнивался к T k 2 . Отсюда получаем, что 0 < k 2 < 1 дает понять, что график функции увеличивает период по О х, при k 1 уменьшает его. От коэффициента k 1 зависит амплитуда колебаний синусоиды и косинусоиды.

Рассмотрим примеры решения заданий с преобразованиями y = sin x .

Пример 4

Построить график y = - 3 sin 1 2 x - 3 2 - 2 с помощью преобразований функции y=sinx.

Решение

Необходимо привести функцию к виду ± k 1 · f ± k 2 · x + a + b . Для этого:

y = - 3 sin 1 2 x - 3 2 - 2 = - 3 sin 1 2 (x - 3) - 2

Видно, что k 1 = 3 , k 2 = 1 2 , a = - 3 , b = - 2 . Так как перед k 1 имеется « - » , а перед k 2 - нет, тогда получим цепочку преобразований вида:

y = sin (x) → y = 3 sin (x) → y = 3 sin 1 2 x → y = - 3 sin 1 2 x → → y = - 3 sin 1 2 x - 3 → y = - 3 sin 1 2 (x - 3) - 2

Подробное преобразование синусоиды. При построении графика исходной синусоиды y = sin (x) получаем, что наименьшим положительным периодом считается T = 2 π . Нахождение максимума в точках π 2 + 2 π · k ; 1 , а минимума - - π 2 + 2 π · k ; - 1 , k ∈ Z .

Производится растягивание по О у втрое, значит возрастание амплитуды колебаний возрастет в 3 раза. T = 2 π - это наименьший положительный период. Максимумы переходят в π 2 + 2 π · k ; 3 , k ∈ Z , минимумы - - π 2 + 2 π · k ; - 3 , k ∈ Z .

При растягивании по О х вдвое получаем, что наименьший положительный период увеличивается в 2 раза и равняется T = 2 π k 2 = 4 π . Максимумы переходят в π + 4 π · k ; 3 , k ∈ Z , минимумы – в - π + 4 π · k ; - 3 , k ∈ Z .

Изображение производится симметрично относительно О х. Наименьший положительный период в данном случае не меняется и равняется T = 2 π k 2 = 4 π . Переход максимума выглядит как - π + 4 π · k ; 3 , k ∈ Z , а минимума – π + 4 π · k ; - 3 , k ∈ Z .

Производится сдвижение графика вниз на 2 единицы. Изменение наименьшего общего периода не происходит. Нахождение максимумов с перехождением в точки - π + 3 + 4 π · k ; 1 , k ∈ Z , минимумов - π + 3 + 4 π · k ; - 5 , k ∈ Z .

На данном этапе график тригонометрической функции считается преобразованным.

Рассмотрим подробное преобразование функции y = cos x .

Пример 5

Построить график функции y = 3 2 cos 2 - 2 x + 1 при помощи преобразования функции вида y = cos x .

Решение

По алгоритму необходимо заданную функцию привести к виду ± k 1 · f ± k 2 · x + a + b . Тогда получаем, что

y = 3 2 cos 2 - 2 x + 1 = 3 2 cos (- 2 (x - 1)) + 1

Из условия видно, что k 1 = 3 2 , k 2 = 2 , a = - 1 , b = 1 , где k 2 имеет « - » , а перед k 1 он отсутствует.

Отсюда получаем, что получится график тригонометрической функции вида:

y = cos (x) → y = 3 2 cos (x) → y = 3 2 cos (2 x) → y = 3 2 cos (- 2 x) → → y = 3 2 cos (- 2 (x - 1)) → y = 3 2 cos - 2 (x - 1) + 1

Пошаговое преобразование косинусоиды с графической иллюстрацией.

При заданной графике y = cos (x) видно, что наименьший общий период равняется T = 2 π . Нахождение максимумов в 2 π · k ; 1 , k ∈ Z , а минимумов π + 2 π · k ; - 1 , k ∈ Z .

При растягивании вдоль О у в 3 2 раза происходит возрастание амплитуды колебаний в 3 2 раза. T = 2 π является наименьшим положительным периодом. Нахождение максимумов в 2 π · k ; 3 2 , k ∈ Z , минимумов в π + 2 π · k ; - 3 2 , k ∈ Z .

При сжатии вдоль О х вдвое получаем, что наименьшим положительным периодом является число T = 2 π k 2 = π . Производится переход максимумов в π · k ; 3 2 , k ∈ Z ,минимумов - π 2 + π · k ; - 3 2 , k ∈ Z .

Симметричное отображение относительно О у. Так как график нечетный, то он не будет изменяться.

При сдвигании графика на 1 . Отсутствуют изменения наименьшего положительного периода T = π . Нахождение максимумов в π · k + 1 ; 3 2 , k ∈ Z , минимумов - π 2 + 1 + π · k ; - 3 2 , k ∈ Z .

При сдвигании на 1 наименьший положительный период равняется T = π и не изменен. Нахождение максимумов в π · k + 1 ; 5 2 , k ∈ Z , минимумов в π 2 + 1 + π · k ; - 1 2 , k ∈ Z .

Преобразования функции косинуса завершено.

Рассмотрим преобразования на примере y = t g x .

Пример 6

Построить график функции y = - 1 2 t g π 3 - 2 3 x + π 3 при помощи преобразований функции y = t g (x) .

Решение

Для начала необходимо привести заданную функцию к виду ± k 1 · f ± k 2 · x + a + b , после чего получаем, что

y = - 1 2 t g π 3 - 2 3 x + π 3 = - 1 2 t g - 2 3 x - π 2 + π 3

Отчетливо видно, что k 1 = 1 2 , k 2 = 2 3 , a = - π 2 , b = π 3 , а перед коэффициентами k 1 и k 2 имеется « - » . Значит, после преобразования тангенсоиды получаем

y = t g (x) → y = 1 2 t g (x) → y = 1 2 t g 2 3 x → y = - 1 2 t g 2 3 x → → y = - 1 2 t g - 2 3 x → y = - 1 2 t g - 2 3 x - π 2 → → y = - 1 2 t g - 2 3 x - π 2 + π 3

Поэтапное преобразование тангенсоиды с графическим изображением.

Имеем, что исходный график – это y = t g (x) . Изменение положительного периода равняется T = π . Областью определения считается - π 2 + π · k ; π 2 + π · k , k ∈ Z .

Сжимаем в 2 раза вдоль О у. T = π считается наименьшим положительным периодом, где область определения имеет вид - π 2 + π · k ; π 2 + π · k , k ∈ Z .

Растягиваем вдоль О х в 3 2 раза. Вычислим наименьший положительный период, причем равнялся T = π k 2 = 3 2 π . А область определения функции с координатами - 3 π 4 + 3 2 π · k ; 3 π 4 + 3 2 π · k , k ∈ Z , меняется только область определения.

Симметрия идет по сторону О х. Период не изменится в этот момент.

Необходимо симметрично отображать оси координат. Область определения в данном случае неизменна. График совпадает с предыдущим. Это говорит о том, что функция тангенса нечетная. Если к нечетной функции задать симметричное отображение О х и О у, тогда преобразуем до исходной функции.

Решение

Для начала необходимо перейти от арккосинуса к арксинусу при помощи обратных тригонометрических функций a r c sin x + a r c o cos x = π 2 . Значит, получим, что a r c sin x = π 2 - a r c cos x .

Видно, что y = a r c cos x → y = - a r c cos x → y = - a r c cos x + π 2 .

Поэтапное преобразование арккосинуса и графическое изображение.

График, данный по условию

Производим отображение относительно О х

Производим движение вверх на π 2 .

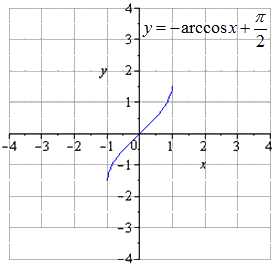
Таким образом, осуществляется переход от арккосинуса к косинусу. Необходимо произвести геометрические преобразования арксинуса и его графика.

Видно, что k 1 = 2 , k 2 = 1 3 , a = - 1 , b = 0 , где отсутствует знак « - » у k 1 и k 2 .

Отсюда получаем, что преобразования y = a r c sin x примет вид:

y = a r c sin (x) → y = 2 a r c sin (x) → → y = 2 a r c sin 1 3 x → y = 2 a r c sin 1 3 (x - 1)

Поэтапное преобразование графика арксинуса и графическое изображение.

График y = a r c sin x имеет область определения вида x ∈ - 1 ; 1 , тогда интервал y ∈ - π 2 ; π 2 относится к области значений.

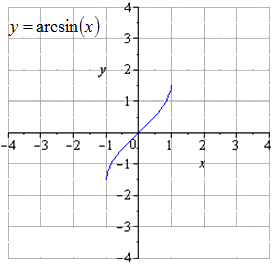
Необходимо растянуть вдвое по О у, причем область определения останется неизменной x ∈ - 1 ; 1 , а область значений y ∈ - π ; π .

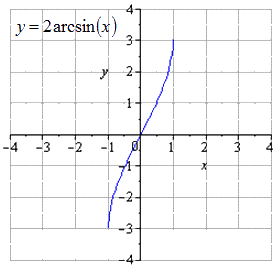
Растягивание по О х строе. Происходит расширение области определения x ∈ - 3 ; 3 , но область значений остается неизменной y ∈ - π ; π .

, Конкурс «Презентация к уроку»

Презентация к уроку

Назад Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цель урока: Определить закономерности преобразования графиков функций.

Задачи:

Образовательная:

• Научить обучающихся строить графики функций путем преобразования графика данной функции, применяя параллельный перенос, сжатие (растяжение), различные виды симметрии.

Воспитательная:

• Воспитывать личностные качества обучающихся (умение слушать), доброжелательность по отношению к окружающим, внимательность, аккуратность, дисциплинированность, умение работать в группе.
• Воспитывать интерес к предмету и потребности в приобретении знаний.

Развивающая:

• Развивать пространственное воображение и логическое мышление обучающихся, умение быстро ориентироваться в обстановке; развивать сообразительность, находчивость, тренировать память.

Оборудование:

• Мультимедийная установка: компьютер, проектор.

Литература:

1. Башмаков, М. И. Математика [Текст]: учебник для учреждений нач. и сред. проф. образования/ М. И. Башмаков.- 5-е изд., испр. – М.: Издательский центр “Академия”, 2012. – 256 с.
2. Башмаков, М. И. Математика. Задачник [Текст]: учеб. пособие для образоват. учреждений нач. и сред. проф. образования/ М. И. Башмаков.– М.: Издательский центр “Академия”, 2012. – 416 с.

План урока:

1. Организационный момент (3 мин).
2. Актуализация знаний (7 мин).
3. Объяснение нового материала (20 мин).
4. Закрепление нового материала (10 мин).
5. Итог урока (3 мин).
6. Домашнее задание (2 мин).

Ход урока

1. Орг. момент (3 мин).

Проверка присутствующих.

Сообщение цели урока.

Основные свойства функций как зависимостей между переменными величинами не должны существенно меняться при изменении способа измерения этих величин, т. е. при изменении масштаба измерения и начала отсчета. Однако за счет более рационального выбора способа измерения переменных величин обычно удается упростить запись зависимости между ними, привести эту запись к некоторому стандартному виду. На геометрическом языке изменение способа измерения величин означает некоторые простые преобразования графиков, к изучению которых мы сегодня и перейдем.

2. Актуализация знаний (7 мин).

Прежде чем будем говорить о преобразованиях графиков, повторим пройденный материал.

Устная работа. (Слайд 2).

Даны функции:

3. Охарактеризуйте графики функций: , , , .

3. Объяснение нового материала (20 мин).

Простейшие преобразования графиков – это их параллельный перенос, сжатие (растяжение) и некоторые виды симметрии. Некоторые преобразования представлены в таблице (Приложение 1) , (Слайд 3).

Работа в группах.

Каждая группа строит графики заданных функций и представляет результат для обсуждения.

Функция	Преобразование графика функции	Примеры функций	Слайд
	Оу на А единиц вверх, если A >0, и на |A| единиц вниз, если А <0.	,	(Слайд 4)
	Параллельный перенос его вдоль оси Ох на а единиц вправо, если а >0, и на -а единиц влево, если а <0.	,	(Слайд 5)
,

ДАГЕСТАНСКИЙ ИНСТИТУТ ПОВЫШЕНИЯ КВАЛИФИКАЦИИ

ПЕДАГОГИЧЕСКИХ КАДРОВ

КАФЕДРА ФИЗИКО- МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ И ИКТ

Проект

на тему:

« Построение и п реобразования

графиков функций

в школьном курсе математики »

Рабаданова П.А.

учитель математики

МБОУ « Кочубейская СОШ»

Тарумовский район

2015 г.

1. Введение……………………………………………………………….….3

2. Глава I . Обзор литературы по теме проекта………………………….….5

3. Глава II . Эмпирическая часть:

3.1. Основные методы преобразования графиков функции……….….7

3.2. Построение графиков четной и нечетной функций…………….. 10

3.3. Построение графика обратной функции………………………... 11

3.4. Деформация (сжатие и растяжение) графиков ………………….12

3.5.Комбинация переноса, отражения и деформации………………......13

4.Задания для самостоятельного решения………………………..…...14

5.Заключение………………………………………………………………15

6. Выводы…………………………………………………………..………17

ВВЕДЕНИЕ

Преобразование графиков функции является одним из фундаментальных математических понятий, непосредственно связанные с практической деятельностью. В графиках отражены изменчивость и динамичность реального мира, взаимные отношения реальных объектов и явлений.

Функциональная линия является базовой тематикой, рассматриваемая в Основном и Едином государственных экзаменах. Так же многие математические понятия рассматриваются графическими методами. Например, к вадратичная функция вводится и изучается в тесной связи с квадратными уравнениями и неравенствами. Отсюда следует, что обучение учащихся построению и преобразованию графиков функции является одной из главных задач обучению математике в школе.

Исследование функции дает возможность найти об ласть определения и область значения функции, обла сти убывания или возрастания, асимптоты, интервалы знакопостоянства и др. Однако для построения графи ков многих функций можно использовать ряд методов, облегча ющие построение. Поэтому учащиеся должны иметь компетенции построения графиков по методическим схемам.

Выше сказанное определяет актуальность темы исследования.

Объектом исследования является изучение преобразование графиков функциональной линии в школьной математике.

Предмет исследования – процесс построение и преобразование графиков функции в общеобразовательной школе.

Цель исследования: образовательная - заключается в выявлении методической схемы построения и преобразования графиков функции; развивающая - развитие абстрактного, алгоритмического, логического мышления, пространственного воображения; воспитательная – воспитание графической культуры школьников, формирование навыков умственного труда.

Цели обусловили решение следующих задач:

1. Проанализировать учебно-методическую по исследуемой проблеме.

2. Выявить методические схемы преобразования графиков функции в школьном курсе математики.

3. Отобрать наиболее эффективные методы и средства построение и преобразование графиков функции в общеобразовательной школе , способствующие: осмысленному усвоению учебного материала; повышению познавательной активности учащихся; развитию их творческих способностей.

ГИПОТЕЗА исследования: формирование графических навыков в процессе изучения функций и воспитание графической культуры учащихся будет эффективным, если учащиеся владеют методической схемой построения и преобразования графиков функции в школьном курсе математики.

ГЛАВА I . ОБЗОР ЛИТЕРАТУРЫ ПО ТЕМЕ ПРОЕКТА.

При подготовке к проекту мы изучили следующую литературу:

Сивашинский, И. Х. Теоремы и задачи по алгебре, элементарным функциям - М., 2002. - 115 с.

Гельфанд, И. М., Глаголева, Е. Г., Шноль, Э. Э. Функции и графики (основные приемы) - М., 1985. - 120 с

В.З.Зайцев, В.В. Рыжков, М.И. Сканави. Элементарная математика- М., 2010(переиздание). - 590 с.

Кузьмин, М. К. Построение графика функции - Ж. Математика в школе. - 2003. - №5. - С. 61-62.

Шилов Г.Е. Как строить графики? - М., 1982.

Исаак Танатар. Геометрические преобразования графиков функций - МЦНМО, 2012

В отмечено, что умение с помощью графика «прочитать» поведение функции на некотором множестве находит применение не только в курсе математики, но и в любой практической деятельности человека, в которой ему приходится иметь дело с теми или иными графическими изображениями зависимостей. Поэтому учащиеся должны уметь по графику функции определить некоторые ее свойства.

В строго изложен теоретический материал преобразования графиков. Сопровождается методика иллюстрацией рисунками, различной сложности примерами и их решениями, что дает возможность углублено расширить знания и построении графиков сложных функций.

Представляет электронный учебный курс, объем и содержание которого соответствуют требованиям к курсу математики старших классов средней школы. Теоретический материал подкреплен графическими анимационными иллюстрациями, которые дают наглядные представления об изучаемой теме. Курс включает три модуля: модуль изучения теоретического материала, модуль самопроверки и модуль контроля знаний.

Из , , использованы для эмпирической части проекта методические схемы построения графиков, примеры для самостоятельной работы.

Выводы к 1 главе

Изучение учебно-методической литературы позволило:

1. Выявить методическую схему изучения, построения и преобразования графиков функции в школьном курсе математики.

2. Отобрать наиболее эффективные методы и средства построение и преобразование графиков функции в школьной математике, способствующие:

осмысленному усвоению учебного материала;

повышению познавательной активности учащихся;

развитию их творческих способностей.

3. показать, что функциональная линия оказывает существенное влияние при изучении различных понятий в математике.

Глава 2. ЭМПИРИЧЕСКАЯ ЧАСТЬ

В этой главе мы рассмотрим основные методы преобразования графиков функций, дадим методические схемы построения различных комбинаций графиков для различных функций.

2.1. ОСНОВНЫЕ МЕТОДЫ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИИ

Перенос вдоль оси ординат

f ( x ) f ( x )+ b .

Для построения графика функции y = f ( x ) + b следу ет:

1. построить график функции y = f ( x )

2. перенести ось абсцисс на | b | единиц вверх при b >0 или на | b | еди ниц вниз при b < 0. Полученный в новой системе коор динат график является графиком функции y = f ( x ) + b .

2. Перенос вдоль оси абсцисс

f ( x ) f ( x + a ) .

y = f ( x + a ) следу ет:

3. Построение графика функции вида y = f (- x )

f (x ) f (- x ).

Для построения графика функции y = f ( - х) следует:

построить график функции y = f ( x )

отразить его отно сительно оси ординат

полученный график является графиком функции y = f ( - х).

4. Построение графика функции вида у = - f ( x )

f ( x ) - f ( x )

- f ( x ) следует:

построить график функции y = f ( x )

отразить его относительно оси абсцисс

2.2. Построение графиков четной и нечетной функций

При построении графиков четной и нечетной функции удобно пользоваться следующими свойствами:

1.График четной функции симмет ричен относительно оси ординат.

2. График нечетной функции симметричен относительно начала координат.

Для построения графиков четной и нечетной функции достаточно построить только правую ветвь графика для положительных значений аргумента. Левая ветвь достраивается симметрично относительно начала координат для нечетной функции и относительно оси ординат для четной функции.

Для построения графика четной функции y = f ( x ) сле дует:

построить ветвь графика этой функции только в об ласти положительных значений аргумента х≥О.

О тразить этот ветвь относительно оси ординат

Для построения графика нечетной функции y = f ( x ) следует:

строить ветвь графика этой функции только в области положительных значений аргумента (х≥0).

О тразить этот ветвь относительно начало координат в область отрицательных значений х.

2.3. Построение графика обратной функции

Как уже отмечалось, прямая и обратная функции вы ражают одну и ту же зависимость между переменными х и у, с тем только отличием, что в обратной функции эти переменные поменялись ролями, что равносильно изме нению обозначений осей координат. Поэтому график обратной функции симметричен графику прямой функции относительно биссектрисы I и III координатных углов, т. е. относительно прямой у = х. Таким образом, получаем следующее правило.

Для построения графика функции у = (х), обратной по отношению к функции y = f ( x ), следует построить график y = f ( x ) и отразить его относительно прямой у = х.

2.4. Деформация (сжатие и растяжение) графиков

1. Сжатие (растяжение) графика вдоль оси ординат

f ( x ) A ∙ f ( x ).

Для построения графика функции y = A ∙ f ( x ) следует:

8. Сжатие (растяжение) графика вдоль оси абсцисс

f ( x )

Для построения графика функции у = f ( x ) следует:

2.5. Комбинация переноса, отражения и деформации

Очень часто при построении графиков функций при меняют комбинацию приемов .

Последовательное применение ряда таких приемов поз воляет существенно упростить построение графика ис ходной функции и нередко свести его в конце концов к построению одной из простейших элементарных функ ций. Рассмотрим, как с учетом изложенного следует строить графики функций.

Отметим, что поря док упрощения целесообразно проводить в следующей последователь ности.

Использование четности или нечетности функции.

Перенос осей.

Отражение и деформация.

Построение же графика выполняется в обратной последовательности.

Пример. Построить график функции

Построение проведем по следующим шагам:

1. построим график натурального логарифма :

2. сожмём к оси OY в 2 раза: ;
3. отобразим симметрично относительно оси OY : ;
4. сдвинем вдоль оси OX на (!!!) вправо: :

5. отобразим симметрично относительно оси OX : ;
6. сдвинем вдоль оси OY на 3 единицы вверх: :

ПРИМЕРЫ ПОСТРОЕНИЯ и ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИИ

Пример 1. Построить график функции .

Сначала изобразим график синуса, его период равен :

график функции получается путём сжатия графика к оси ординат в два раза. log .

Построить график функции у = 2 cos х.

Построить график функции y = sin x .

ЗАКЛЮЧЕНИЕ

Во время работы над проектной работой были проанализирована различная учебно-методическая литература по данной проблеме. Результаты исследования позволили выявить наиболее характерные положительные стороны изучения , построения и преобразования графиков функции в школьном курсе математики

Основной целью проекта является формирование у учащихся умений и навыков в чтении и выполнении чертежей, в формировании у них рациональных приемов самостоятельной деятельности.

Необходимость усовершенствования графического образования в целом диктуется не только современными требованиями производства, но и ролью графики в развитии технического мышления и познавательных способностей учащихся. Способность человека к переработке графической информации является одним из показателей его умственного развития. Поэтому графическая подготовка должна стать неотъемлемым элементом общеобразовательной подготовки.

Выводы

Таким образом, разработанный проект « Построение и преобразование графиков функции», посвященный одному из центральных понятий математики - функциональной зависимости, ориентирован на систематизацию и расширение знаний учащихся. Изучение конкретных способов преобразования графиков функций проводится аналитико-графическим путем по строгим методическим схемам. Собранный материал можно использовать на уроках и для самоподготовки учащихся. Для проведения занятий могут использоваться разнообразные формы и методы организации и обучения.

Параллельный перенос.

ПЕРЕНОС ВДОЛЬ ОСИ ОРДИНАТ

f(x) => f(x) - b
Пусть требуется построить график функции у = f(х) - b. Нетрудно заметить, что ординаты этого графика для всех значений x на |b| единиц меньше соответствующих ординат графика функций у = f(х) при b>0 и на |b| единиц больше - при b 0 или вверх при b Для построения графика функции y + b = f(x) следует построить график функции y = f(x) и перенести ось абсцисс на |b| единиц вверх при b>0 или на |b| единиц вниз при b

ПЕРЕНОС ВДОЛЬ ОСИ АБСЦИСС

f(x) => f(x + a)
Пусть требуется построить график функции у = f(x + a). Рассмотрим функцию y = f(x), которая в некоторой точке x = x1 принимает значение у1 = f(x1). Очевидно, функция у = f(x + a) примет такое же значение в точке x2, координата которой определяется из равенства x2 + a = x1, т.е. x2 = x1 - a, причем рассматриваемое равенство справедливо для совокупности всех значений из области определения функции. Следовательно, график функции у = f(x + a) может быть получен параллельным перемещением графика функции y = f(x) вдоль оси абсцисс влево на |a| единиц при a > 0 или вправо на |a| единиц при a Для построения графика функции y = f(x + a) следует построить график функции y = f(x) и перенести ось ординат на |a| единиц вправо при a>0 или на |a| единиц влево при a

Примеры:

1.y=f(x+a)

2.y=f(x)+b

Отражение.

ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ ВИДА Y = F(-X)

f(x) => f(-x)
Очевидно, что функции y = f(-x) и y = f(x) принимают равные значения в точках, абсциссы которых равны по абсолютной величине, но противоположны по знаку. Иначе говоря, ординаты графика функции y = f(-x) в области положительных (отрицательных) значений х будут равны ординатам графика функции y = f(x) при соответствующих по абсолютной величине отрицательных (положительных) значениях х. Таким образом, получаем следующее правило.
Для построения графика функции y = f(-x) следует построить график функции y = f(x) и отразить его относительно оси ординат. Полученный график является графиком функции y = f(-x)

ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ ВИДА Y = - F(X)

f(x) => - f(x)
Ординаты графика функции y = - f(x) при всех значениях аргумента равны по абсолютной величине, но противоположны по знаку ординатам графика функции y = f(x) при тех же значениях аргумента. Таким образом, получаем следующее правило.
Для построения графика функции y = - f(x) следует построить график функции y = f(x) и отразить его относительно оси абсцисс.

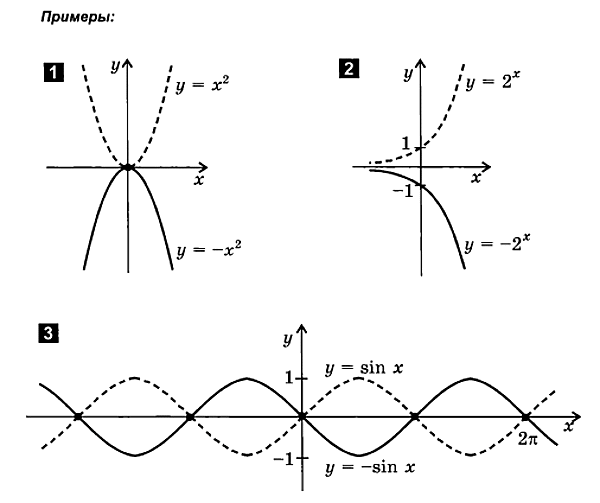
Примеры:

1.y=-f(x)

2.y=f(-x)

3.y=-f(-x)

Деформация.

ДЕФОРМАЦИЯ ГРАФИКА ВДОЛЬ ОСИ ОРДИНАТ

f(x) => k f(x)
Рассмотрим функцию вида y = k f(x), где k > 0. Нетрудно заметить, что при равных значениях аргумента ординаты графика этой функции будут в k раз больше ординат графика функции у = f(x) при k > 1 или 1/k раз меньше ординат графика функции y = f(x) при k Для построения графика функции y = k f(x) следует построить график функции y = f(x) и увеличить его ординаты в k раз при k > 1(произвести растяжение графика вдоль оси ординат) или уменьшить его ординаты в 1/k раз при k
k > 1 - растяжение от оси Ох
0 - сжатие к оси OX

ДЕФОРМАЦИЯ ГРАФИКА ВДОЛЬ ОСИ АБСЦИСС

f(x) => f(k x)
Пусть требуется построить график функции y = f(kx), где k>0. Рассмотрим функцию y = f(x), которая в произвольной точке x = x1 принимает значение y1 = f(x1). Очевидно, что функция y = f(kx) принимает такое же значение в точке x = x2, координата которой определяется равенством x1 = kx2, причем это равенство справедливо для совокупности всех значений х из области определения функции. Следовательно, график функции y = f(kx) оказывается сжатым (при k 1) вдоль оси абсцисс относительно графика функции y = f(x). Таким образом, получаем правило.
Для построения графика функции y = f(kx) следует построить график функции y = f(x) и уменьшить его абсциссы в k раз при k>1 (произвести сжатие графика вдоль оси абсцисс) или увеличить его абсциссы в 1/k раз при k
k > 1 - сжатие к оси Оу
0 - растяжение от оси OY

Работу выполнили Чичканов Александр, Леонов Дмитрий под руководством Ткач Т.В, Вязовова С.М, Островерховой И.В.
©2014

Преобразование графиков функций

В этой статье я познакомлю вас с линейными преобразованиями графиков функций и покажу, как с помощью этих преобразований из графика функции получить график функции

Линейным преобразованием функции называется преобразование самой функции и/или ее аргумента к виду , а также преобразование, содержащее модуль аргумента и/или функции.

Наибольшие затруднения при построении графиков с помощью линейных преобразований вызывают следующие действия:

1. Вычленение базовой функции, собственно, график которой мы и преобразовываем.
2. Определения порядка преобразований.

И менно на этих моментах мы и остановимся подробнее.

Рассмотрим внимательно функцию

В ее основе лежит функция . Назовем ее базовой функцией .

При построении графика функции мы совершаем преобразования графика базовой функции .

Если бы мы совершали преобразования функции в том же порядке, в каком находили ее значение при определенном значении аргумента, то

Рассмотрим какие виды линейных преобразований аргумента и функции существуют, и как их выполнять.

Преобразования аргумента.

1. f(x) f(x+b)

1. Строим график фунции

2. Сдвигаем график фунции вдоль оси ОХ на |b| единиц

• влево, если b>0
• вправо, если b<0

Построим график функции

1. Строим график функции

2. Сдвигаем его на 2 единицы вправо:

2. f(x) f(kx)

1. Строим график фунции

2. Абсциссы точек графика делим на к, ординаты точек оставляем без изменений.

Построим график функции .

1. Строим график функции

2. Все абсциссы точек графика делим на 2, ординаты оставляем без изменений:

3. f(x) f(-x)

1. Строим график фунции

2. Отображаем его симметрично относительно оси OY.

Построим график функции .

1. Строим график функции

2. Отображаем его симметрично относительно оси OY:

4. f(x) f(|x|)

1. Строим график функции

2. Часть графика, расположенную левее оси ОY стираем, часть графика, расположенную правее оси ОY Достраиваем симметрично относительно оси OY:

График функции выглядит так:

Построим график функции

1. Строим график функции (это график функции , смещенный вдоль оси ОХ на 2 единицы влево):

2. Часть графика, расположенную левее оси OY (x<0) стираем:

3. Часть графика, расположенную правее оси OY (x>0) достраиваем симметрично относительно оси OY:

Важно! Два главных правила преобразования аргумента.

1. Все преобразования аргумента совершаются вдоль оси ОХ

2. Все преобразования аргумента совершаются "наоборот" и "в обратном порядке".

Например, в функции последовательность преобразований аргумента такая:

1. Берем модуль от х.

2. К модулю х прибавляем число 2.

Но построение графика мы совершали в обратном порядке:

Сначала выполнили преобразование 2. - сместили график на 2 единицы влево (то есть абсциссы точек уменьшили на 2, как бы "наоборот")

Затем выполнили преобразование f(x) f(|x|).

Коротко последовательность преобразований записывается так:

Теперь поговорим о преобразовании функции . Преобразования совершаются

1. Вдоль оси OY.

2. В той же последовательности, в какой выполняются действия.

Вот эти преобразования:

1. f(x)f(x)+D

2. Смещаем его вдоль оси OY на |D| единиц

• вверх, если D>0
• вниз, если D<0

Построим график функции

1. Строим график функции

2. Смещаем его вдоль оси OY на 2 единицы вверх:

2. f(x)Af(x)

1. Строим график функции y=f(x)

2. Ординаты всех точек графика умножаем на А, абсциссы оставляем без изменений.

Построим график функции

1. Построим график функции

2. Ординаты всех точек графика умножим на 2:

3. f(x)-f(x)

1. Строим график функции y=f(x)

Построим график функции .

1. Строим график функции .

2. Отображаем его симметрично относительно оси ОХ.

4. f(x)|f(x)|

1. Строим график функции y=f(x)

2. Часть графика, расположенную выше оси ОХ оставляем без изменений, часть графика, расположенную ниже оси OX, отображаем симметрично относительно этой оси.

Построим график функции

1. Строим график функции . Он получается смещением графика функции вдоль оси OY на 2 единицы вниз:

2. Теперь часть графика, расположенную ниже оси ОХ, отобразим симметрично относительно этой оси:

И последнее преобразование, которое, строго говоря, нельзя назвать преобразованием функции, поскольку результат этого преобразования функцией уже не является:

|y|=f(x)

1. Строим график функции y=f(x)

2. Часть графика, расположенную ниже оси ОХ стираем, затем часть графика, расположенную выше оси ОХ достраиваем симметрично относительно этой оси.

Построим график уравнения

1. Строим график функции :

2. Часть графика, расположенную ниже оси ОХ стираем:

3. Часть графика, расположенную выше оси ОХ достраиваем симметрично относительно этой оси.

И, наконец, предлагаю вам посмотреть ВИДЕОУРОК в котором я показываю пошаговый алгоритм построения графика функции

График этой функции выглядит так: